中学生でも分かる線形回帰の簡単な説明
線形回帰とは学術的な話は置いておいて簡単に説明すると直線を用いて計算を行うということです。直線とは中学レベルで学習する1次元方程式をイメージしてもらえると、分かりやすいかと思います。
ではこの1次元方程式を利用して何を求めるのでしょうか?
それは回帰です。回帰とは数値を予測するもので、例えば株式市場の数値を与えることで、株価の予測を行うことができるようになります。また、他に部屋の広さを与えることで家賃はいくらくらいになるかを予測することも出来ます。このようにあるデータの特徴の傾向から、何かしらの数値を予測することを回帰といいます。
つまり線形回帰とは「線形」+「回帰」であるため、データの特徴の傾向を直線に表して、株価の予測や家賃の予想などの数値のデータを求めるということになります。
具体的な例を示します。
この図は部屋の広さ(横軸)に対応する家賃(縦軸)を表しています。個々の〇が事前に学習させておいた物件です。
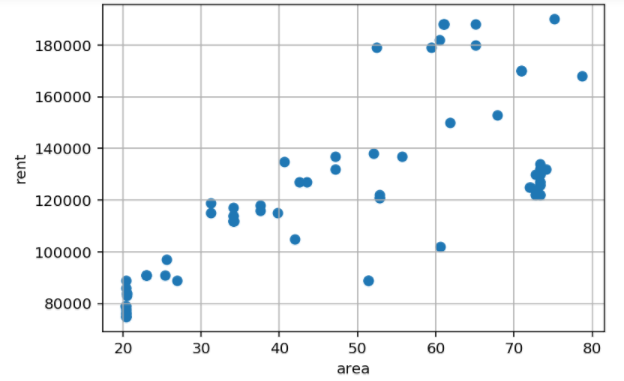
一部例外はありますが、それぞれの〇が左下から右上に伸びています。これは部屋の広さが広くなればなるほど家賃が高くなっているということを示しています。
そこで、なんとなくこんなもんだろうという直線を引いてみます。
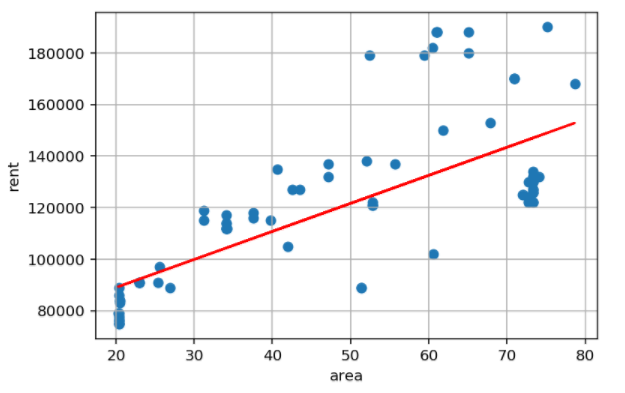
このなんとなくこんなもんだろうという直線が線形回帰となります。
直線が決まったので、部屋の広さが決まれば家賃を求めることができるようになりました。また、家賃が決まれば部屋の広さを求めることができるようになりました。このようにして部屋の広さと家賃の関係性を推測することが可能となります。
ただし、このなんとなくこんなもんだろうというのは人間の場合はある程度感覚で分かる場合がありますが、コンピュータは感覚では分かりません。そのため、全ての〇の点から最も予想が近い点、コスト関数を最小化する最適なパラメータを算出するとも言われますが、小難しい計算式を用いて行われます。
計算式はひとまずおくとして、実際に学習する様子を図で示します。
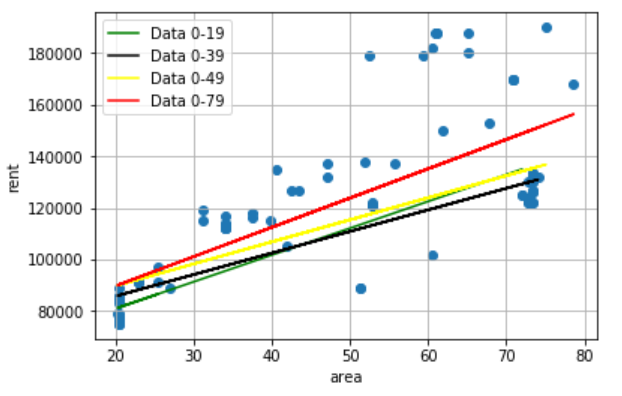
それぞれ物件の数を20個学習した場合、40個学習した場合、60個学習した場合、80個学習した場合のコンピュータが想定した直線です。学習の旅に切片と直線の傾きが変わっていっていることが分かるかと思います。これは学習を増やしていくたびに、コスト関数を最小化する最適なパラメータを調整しているということになります。
このように最適なパラメータに調整した直線を用いて計算するというのが線形回帰となります。