
scikit-learnの機械学習でロジスティック回帰を行い癌の陽性を判断する
scikit-learnを使用した機械学習で、ロジスティク回帰を使用した癌の判定プログラムを行ってみます。
使用するデータはscikit-learnで提供されている癌の判定を行うデータ(load_breast_cancer)です。
このデータは569人分のデータが存在し、凹み,凹点,対称性等の30個の説明変数があります。
またそれぞれの説明変数に対して実際の結果が悪性だったか陽性だったかの目的変数があります。このデータを8割を訓練用に2割を評価用に分割して使用して評価を行ってみます。
使用するデータ
使用データ:scikit-learn(load_breast_cancer)
全データ:569件 (訓練用:8割、評価用:2割に分割)
説明変数:30個(凹み,凹点,対称性・・・)
目的変数::0:悪性/1:陽性
分類/識別:分類(1ラベル)
識別方法:ロジスティク回帰
ソースコード
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#各種ライブラリのImport import numpy as np import pandas as pd from matplotlib import pyplot as pld #%matplotlib inline #scikit-learnより癌のデータを抽出する from sklearn.datasets import load_breast_cancer data = load_breast_cancer() #癌のデータ(説明変数)をdataXに格納する dataX = pd.DataFrame(data=data.data,columns=data.feature_names) dataX.head() #癌のデータ(目的変数)をdataYに格納する dataY = pd.DataFrame(data=data.target) dataY = dataY.rename(columns={0: '判定(0:悪性 / 1:陽性)'}) dataY.head() #データの分割を行う(訓練用データ 0.8 評価用データ 0.2) from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(dataX, dataY, test_size=0.2) #線形モデル(ロジスティク回帰)として測定器を作成する from sklearn import linear_model clf = linear_model.LogisticRegression() #訓練の実施 clf.fit(X_train,y_train) #評価の実行(確率) df = pd.DataFrame(clf.predict_proba(X_test)) df = df.rename(columns={0: '確率(悪性)',1: '確率(陽性)'}) df.head() #評価の実行(判定) df = pd.DataFrame(clf.predict(X_test)) df = df.rename(columns={0: '判定(0:悪性 / 1:陽性)'}) df.head() #混同行列 from sklearn.metrics import confusion_matrix df = pd.DataFrame(confusion_matrix(y_test,clf.predict(X_test).reshape(-1,1), labels=[0,1])) df = df.rename(columns={0: '予想(0)',1: '予想(1)'}, index={0: '実際(0)',1: '実際(1)'}) df #評価の実行(正答率) clf.score(X_test,y_test) #評価の実行(個々の詳細) ng=0 for i,j in zip(clf.predict(X_test),y_test.values.reshape(-1,1)): if i == j: print(i,j,"OK") else: print(i,j,"NG") ng += 1 |
ソースコードの詳細
各種ライブラリのImport
|
1 2 3 4 5 |
#各種ライブラリのImport import numpy as np import pandas as pd from matplotlib import pyplot as pld #%matplotlib inline |
scikit-learnより癌のデータを抽出する
|
1 2 3 |
#scikit-learnより癌のデータを抽出する from sklearn.datasets import load_breast_cancer data = load_breast_cancer() |
癌のデータ(説明変数)をdataXに格納する
|
1 2 3 |
#癌のデータ(説明変数)をdataXに格納する dataX = pd.DataFrame(data=data.data,columns=data.feature_names) dataX.head() |
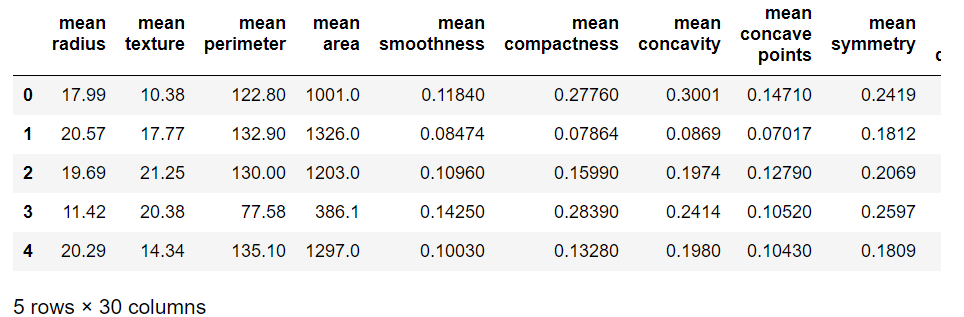
取り出したデータから説明変数となる部分のみを抽出し、dataXという名前のデータフレームに格納しています。
癌のデータ(目的変数)をdataYに格納する
|
1 2 3 4 |
#癌のデータ(目的変数)をdataYに格納する dataY = pd.DataFrame(data=data.target) dataY = dataY.rename(columns={0: '判定(0:悪性 / 1:陽性)'}) dataY.head() |
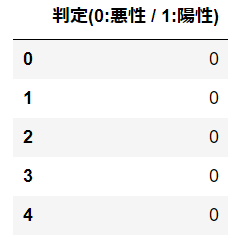
取り出したデータから目的変数となる部分のみを抽出し、dataYという名前のデータフレームに格納しています。
データの分割を行う(訓練用データ 0.8 評価用データ 0.2)
|
1 2 3 |
#データの分割を行う(訓練用データ 0.8 評価用データ 0.2) from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(dataX, dataY, test_size=0.2) |
線形モデル(ロジスティク回帰)として測定器を作成する
|
1 2 3 |
#線形モデル(ロジスティク回帰)として測定器を作成する from sklearn import linear_model clf = linear_model.LogisticRegression() |
訓練の実施
|
1 2 |
#訓練の実施 clf.fit(X_train,y_train) |
|
1 2 3 4 |
LogisticRegression(C=1.0, class_weight=None, dual=False, fit_intercept=True, intercept_scaling=1, max_iter=100, multi_class='ovr', n_jobs=1, penalty='l2', random_state=None, solver='liblinear', tol=0.0001, verbose=0, warm_start=False) |
評価の実行(確率)
|
1 2 3 4 |
#評価の実行(確率) df = pd.DataFrame(clf.predict_proba(X_test)) df = df.rename(columns={0: '確率(悪性)',1: '確率(陽性)'}) df.head() |
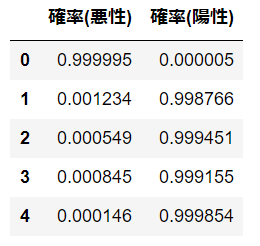
作成したモデルに対して評価を実施します。今回は悪性、陽性のどちらかを判定することが最終目的となりますが、predict_proba関数を使用した場合、それぞれどちらの疑いが強いか確率値を算出することができます。例えば0番目の場合は悪性の確立が99.9995%となっています。逆に2番目~4番目については陽性の確立の方が高くなっています。
評価の実行(判定)
|
1 2 3 4 |
#評価の実行(判定) df = pd.DataFrame(clf.predict(X_test)) df = df.rename(columns={0: '判定(0:悪性 / 1:陽性)'}) df.head() |
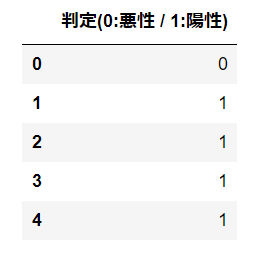
predict関数を使用することで、悪性、陽性のどちらかに分類されるか識別することができます。確率の結果の通り0番目は悪性、2番目~4番目については陽性となっています。
混同行列
|
1 2 3 4 5 |
#混同行列 from sklearn.metrics import confusion_matrix df = pd.DataFrame(confusion_matrix(y_test,clf.predict(X_test).reshape(-1,1), labels=[0,1])) df = df.rename(columns={0: '予想(0)',1: '予想(1)'}, index={0: '実際(0)',1: '実際(1)'}) df |
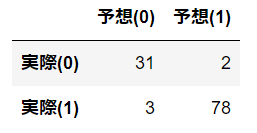
混同行列を行ってみます。混同行列とは縦軸に実際の正解値、横軸に予想の値のクロス表を作成することで、どの程度正解したかどうかを表で分かるようになります。この結果から、実際は0(悪性)のところ1(陽性)と判断されたのは2人になります。逆に1(陽性)のところ0(悪性)と判断されたのは3人になります。
評価の実行(正答率)
|
1 2 |
#評価の実行(正答率) clf.score(X_test,y_test) |
|
1 |
0.95614035087719296 |
評価の実行(個々の詳細)
|
1 2 3 4 5 6 7 8 |
#評価の実行(個々の詳細) ng=0 for i,j in zip(clf.predict(X_test),y_test.values.reshape(-1,1)): if i == j: print(i,j,"OK") else: print(i,j,"NG") ng += 1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 0 [1] NG 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 0 [0] OK 1 [1] OK 0 [1] NG 1 [1] OK 1 [0] NG 1 [1] OK 0 [0] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [0] NG 0 [0] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 0 [0] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 0 [0] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 0 [0] OK 0 [0] OK 1 [1] OK 0 [1] NG 0 [0] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 0 [0] OK 0 [0] OK 0 [0] OK 0 [0] OK 1 [1] OK 0 [0] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK 1 [1] OK |