Confution Matrix(混同行列)とは
AI(人工知能)に欠かせないConfution Matrixについての説明を行います。
Confution Matrixとは混同行列とも呼ばれ、縦軸と横軸の2次元のマトリクス表として表現されます。
このConfution Matrixを調べることで正解率や適合率、検出率、F値などが分かります。
若干、数学が入りますが簡単な式で表現できます。
これらの計算方法を知ることで、正解率が低かった場合でも、何が問題だったのか分析することができるようになり、問題の解決につながります。
是非身に着けてください。
Confution Matrix(混同行列)の例
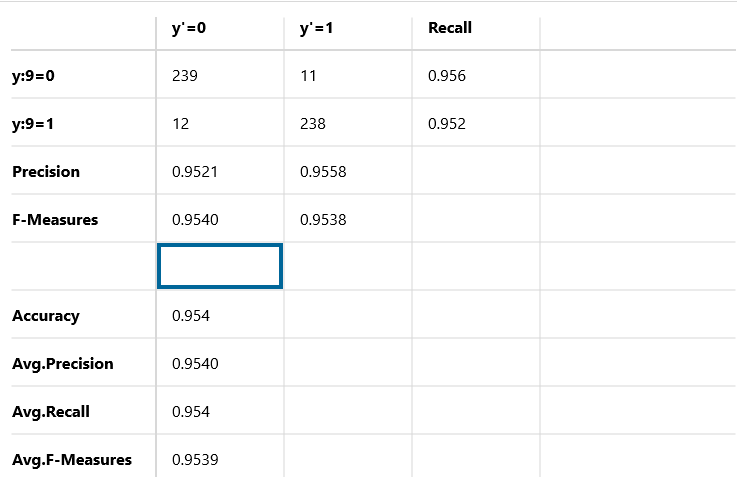
このサンプル画像はNNC(Neural Network Console)で実行した結果を混同行列で表したものです。基本的な見方はTensorflowやKeras、scikit-learnなどに付随しているライブラリで混同行列を表したものと同じものです。
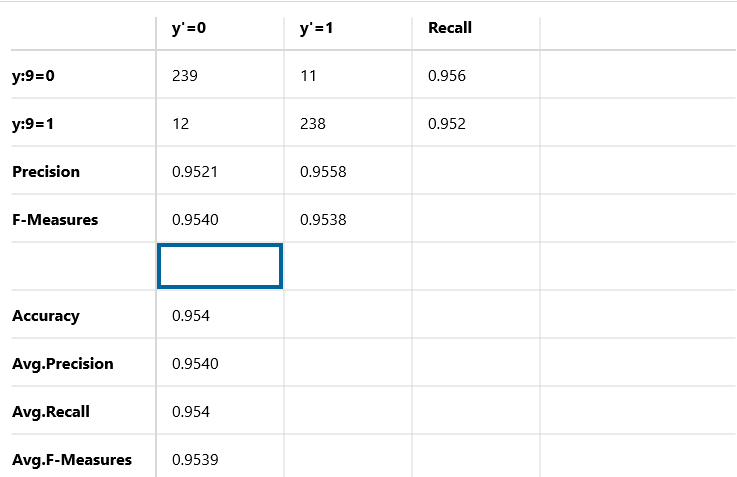
このサンプル画像では4か9のどちらかの数字が書かれているデータをコンピュータに渡し、正しい数字を予想させています。
縦軸は正解のデータを表しています。
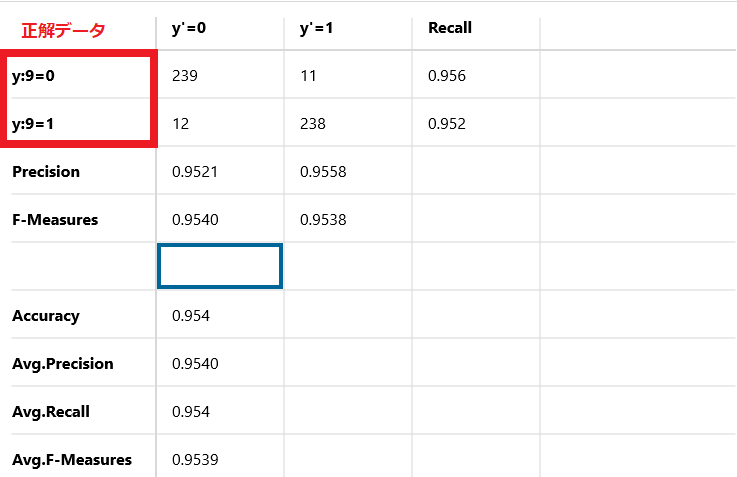
y:9=0と書かれているものが、正解データが4のものです。
y:9=1と書かれているものが、正解データが9のものです。
横軸は予想した結果を示しています。
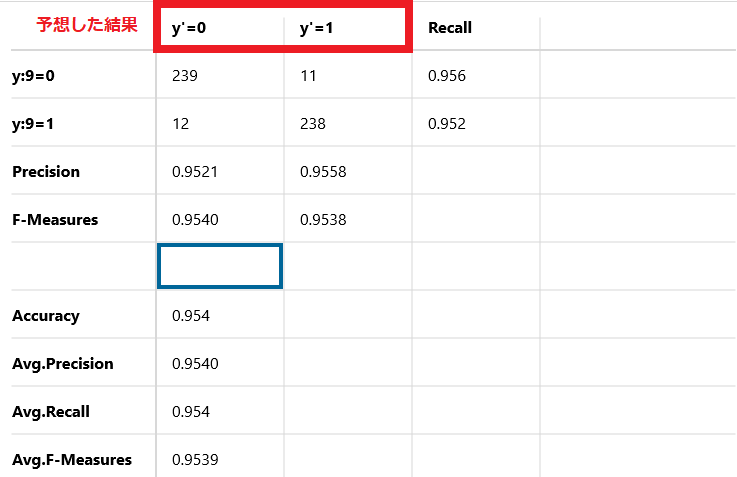
Y'=0と書かれているものが、予想した結果が4のものです。
Y'=1と書かれているものが、予想した結果が9のものです。
この混同行列 (confusion matrix)には4つの概念があります。
True Positive(TP)
正解データと予想したデータが共に真のもの
False Positive(FP)
正解データが真で予想したデータが偽のもの
True Negative(TN)
正解データと予想したデータが共に偽のもの
False Negative(FN)
正解データが偽で予想したデータが真のもの
言葉だと分かりにくいので図で示します。
4という数字をターゲットにした場合
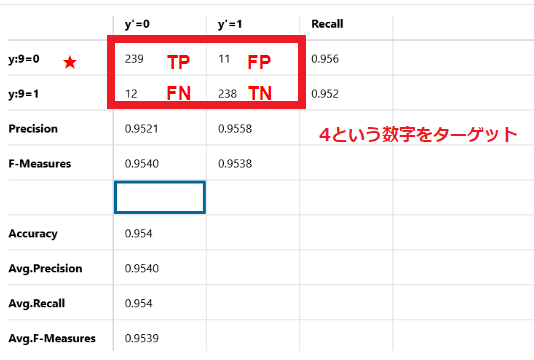
正解データ、予想データがともに4となっているデータが239個存在しています(True Positive)
また正解データが4にも関わらず、誤って9と判定したデータが11個存在しています(False Positive)
9という数字をターゲットにした場合
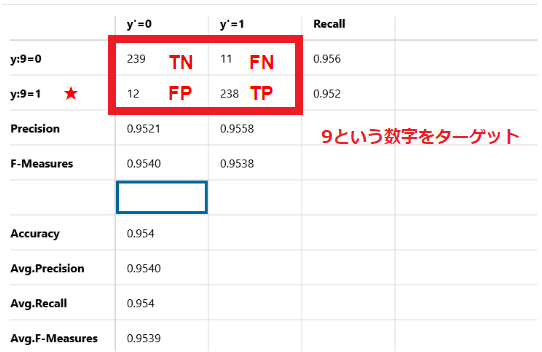
正解データ、予想データがともに9となっているデータが238個存在しています(True Positive)
また正解データが9にも関わらず、誤って4と判定したデータが12個存在しています(False Positive)
Recall
Recallは検出率と呼ばれ、正解のデータの中でどの程度正解したかを示しています。母数は正解のデータです。
計算式
(Recall) = TP/(TP+FN)
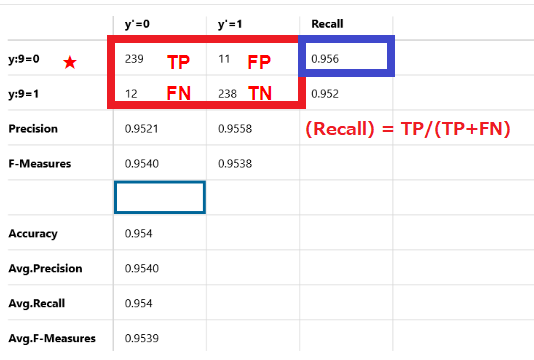
正解が9である250個のデータのうち、239個が正解で11個が不正解です。
Recallは95.6%です。
同様に、
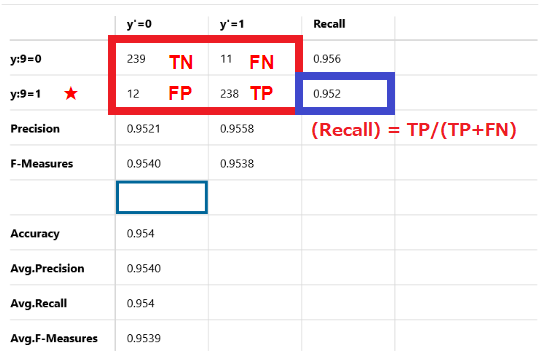
正解が4である250個のデータのうち、238個が正解で12個が不正解です。
Recallは95.2%です。
Precision
Precisionは適合率または精度と呼ばれ、推測したデータの中でどの程度正解したかを示しています。母数は推測した結果になります。
計算式
(Precision) = TP/(TP+FP)
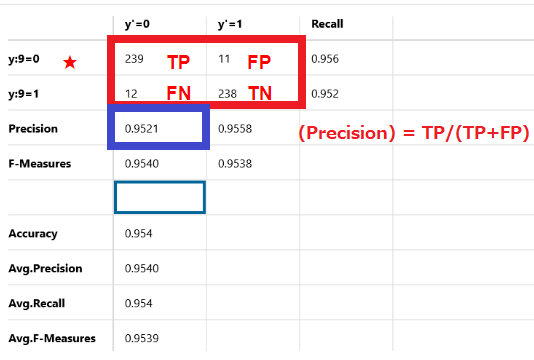
251個のデータを正解を4と推測しましたが、正解したのは239個で不正解は12個です。Precisionは95.21%です。
同様に、
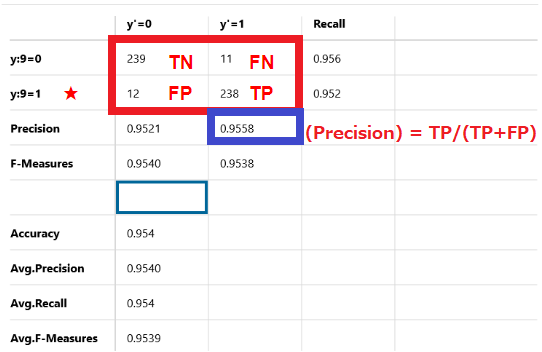
249個のデータを正解を9と推測しましたが、正解したのは238個で不正解は11個です。Precisionは95.58%です。
F-Measures
F-MeasuresはF値またはF尺度と呼ばれ、検出率(Recall)と適合率(Precision)の調和平均を示しています。
調和平均と言うと一見分かりにくいですが、検出率(Recall)と適合率(Precision)のバランスを示しています。高ければ高いほど、検出率(Recall)と適合率(Precision)がともに高くなります。
計算式
(F-Measures) = 2×(Recall)×(Precision) / (Recall) + (Precision)
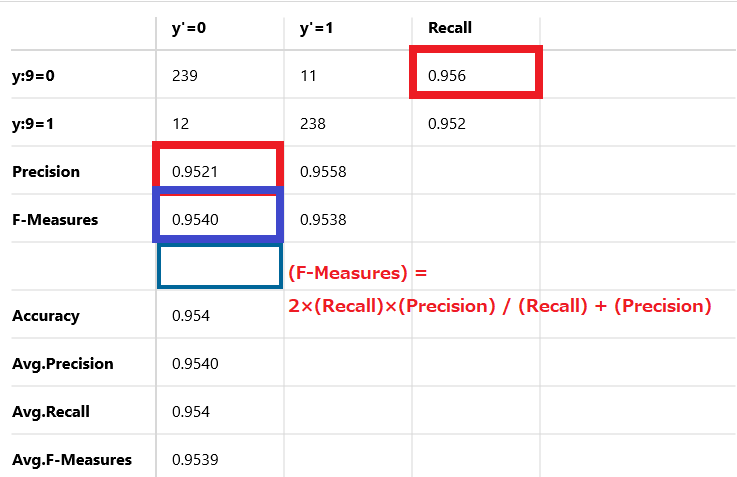
計算式に当てはめてみると1.8204152/1.9081 = 0.9540 となりF値は95.4%を示しています。
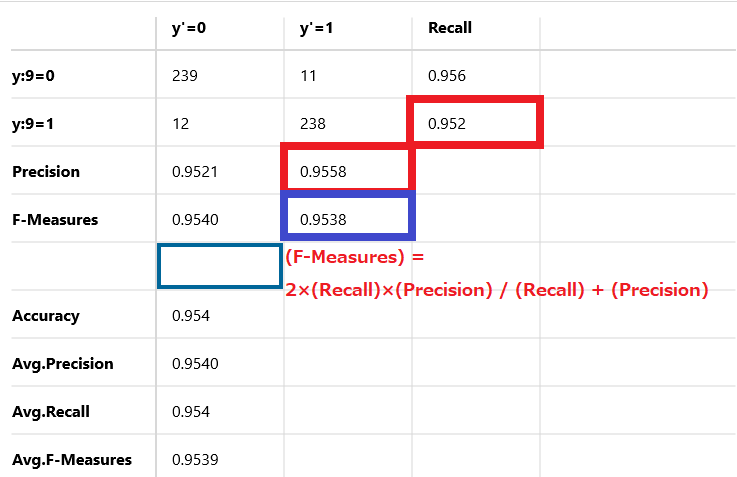
計算式に当てはめてみると1.8198432/1.9078 = 0.9538 となりF値は95.38%を示しています。
F-Measuresは必要なの?
F-Measuresはイメージが湧きずらいため、RecallやPrecisionのどちらかのパーセンテージが高ければ高性能と思うかもしれません。
しかしながら、Recallを100%にすることは簡単にできます。
どのようにするかというと、全ての予想をどちらか一方に偏らせるだけです。
これで簡単に100%になってしまいます。
例えば、4が正解の数値が250個で、9が正解の数値も250個の計500個のデータが存在するとします。その条件で、500個のデータ全てに対して正解は4と予想すればRecallは100%になってしまいます。
しかし、一律全部偏らせたものが高性能であるはずはありません。
そのため、検出率(Recall)と適合率(Precision)のバランスを計算したF-Measuresが必要になります。
Accuracy
計算率
(Accuracy) = (TP+TN)/(TP+FP+FN+TN)
一般的によく使用される正解率です。全てのデータに対して全正解した場合は100%となり、全部不正解だった場合は0%となります。
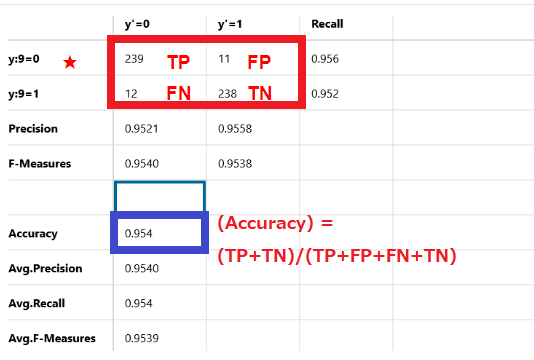
この例では95.4%を示しています。
Avg-Precision
Precision(適合率)の平均です。
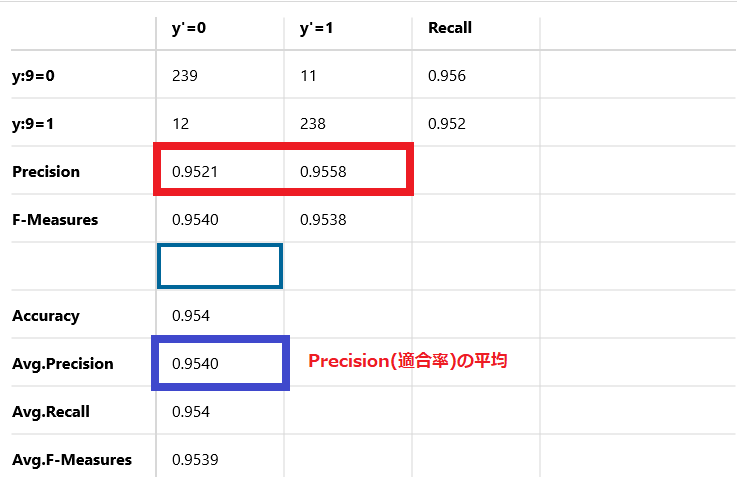
この例では95.4%を示しています。
Avg-Recall
Recall(検出率)の平均です。
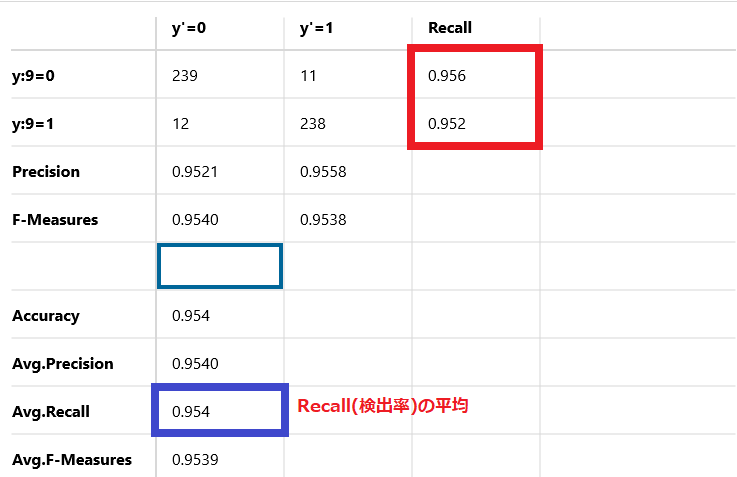
この例では95.4%を示しています。
Avg.F-Measures
F-Measures(F値、F尺度)の平均です。
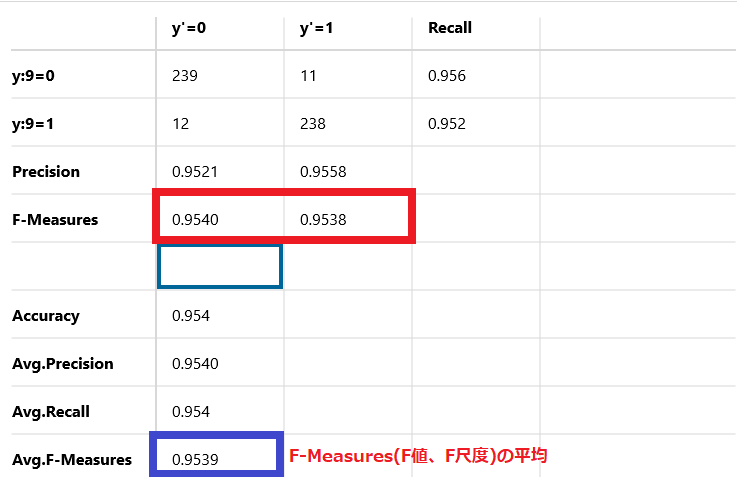
この例では95.39%を示しています。
以上で、Confution Matrix(混同行列)の説明は終了です。このConfution MatrixはTensorflowやKeras、scikit-learnでも同じように計算することができます。
正解率が低かった場合でも、何が悪かったのかの問題の解決につながるので是非身につけておいてください。