今さら聞けないバックプロパゲーションとは
機械学習では神経細胞のネットワークを模倣したニューラルネットワークを用いて推論を行っていきますが、学習の過程で推論と正解値が異なる場合があります。そのまま続けた場合、学習の精度があまり良くない状態となってしまうので、出力結果を元にニューラルネットワーク全体の修正をその都度を行っていく仕組みがあります。その仕組みがバックプロパゲーションと呼ばれる方法です。
バックプロパゲーションは別名、誤差逆伝播法(ごさぎゃくでんぱほう)と呼ばれ、1986年にデビッド・ラメルハートらによって命名されました。バックプロパゲーションの役割はコンピュータの回答が間違っていたり、期待とは離れている場合、誤差を出力側から逆方向に返し、各ニューロンの誤りを正す役割となります。
バックプロパゲーションの具体例
具体的に図を用いて説明します。
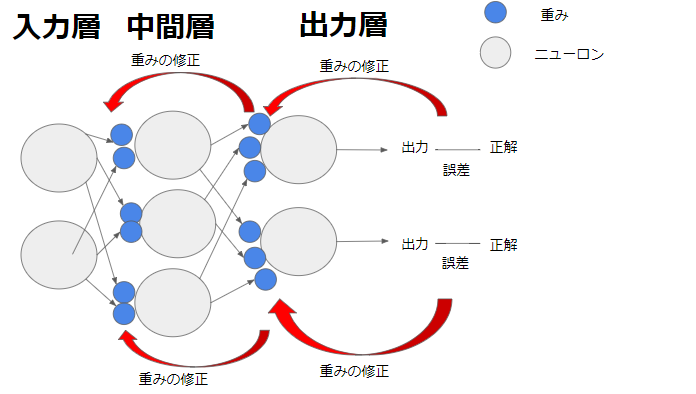
この図は2つのニューロンを持つ入力層と、3つのニューロンを持つ中間層、2つのニューロンを持つ出力層で構成されています。そして中間層と出力層それぞれに重みがあります。仮に、出力層からでた出力値が正解と異なっていた場合、バックプロパゲーションでは出力値と正解の誤差を元に中間層と出力層の間の重みの修正を行います。そしてこの修正値もとに入力層と中間層の間の重みの修正を行っていきます。
このように誤差を元に前の前へとさかのぼっていき修正を行うのがバックプロパゲーションです。
もう一つ例としてMNISTのケースを説明します。
MNISTでは0~9を表している画像データと正解値の0~9の数値データの比較を行います。入力値が画像データで、出力値が0~9の確立値となります。
仮に7を表している画像データを入力した場合、次のように出力値の確立がでる場合があります。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.0xx | 0.62 | 0.0xx | 0.0xx | 0.0xx | 0.0xx | 0.0xx | 0.35 | 0.0xx | 0.0xx |
この場合、正解値が7にも関わらず、出力値の確立は1が最も高くなってしまい不正解となります。不正解となった場合は、バックプロパゲーションを行い重みを修正していきまます。
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0.0xx | 0.30 | 0.0xx | 0.0xx | 0.0xx | 0.0xx | 0.0xx | 0.67 | 0.0xx | 0.0xx |
このように、ニューラルネットワーク全体の修正をその都度行い、学習の精度を高めていってくれるバックプロパゲーションですがいくつか注意点があります。それは4層以上のバックプロパゲーションはうまくいかないということです。一般に層が深くなればなるほど、バックプロパゲーションが下の方まで届かなくなるため、学習の精度が下っていくと言われています。そのため層を増やしすぎない適切な仕組みが必要とされます。