
Alexas_Fotos / Pixabay
ダミー変数とは
ダミー変数とはカテゴリー型のデータを0/1で表現し直す変数のことです。
例えば職業のカテゴリとして、1.事務系、2.医療・看護系・・・6 芸能・芸術系のように定義されている場合に、別なカラム(事務系、.医療・看護系・・・芸能・芸術系)を新しく追加して0/1で表現し直す場合に使用されます。
一般的にカテゴリーデータのような数値に大小の連続性がなく、数値の大小によってパラメータに影響を与えない項目についてはダミー変数に直すといいと言われています。
また、文字列のデータについても同様です。文字列の場合はそのままではデータ分析に使用できません。何かしらの方法で数値に置き替える必要があります。その場合にダミー変数に修正します。
Pandasを用いることで簡単にダミー変数に直すことができます。
実際に例を見た方が分かりやすいかと思いますので下に示します。
ダミー変数の例
ダミー変数の例として次のようなカテゴリがあるとします。職業のカテゴリです。
カテゴリ例
1 事務系
2 医療・看護系
3 教育系
4 営業・販売系
5 公務員系
6 芸能・芸術系
実際のデータは職業というカラムに設定されているとします。

この職業というカラムに対してダミー変数を使用した場合、最終的には以下のように表現をし直すことが出来ます。
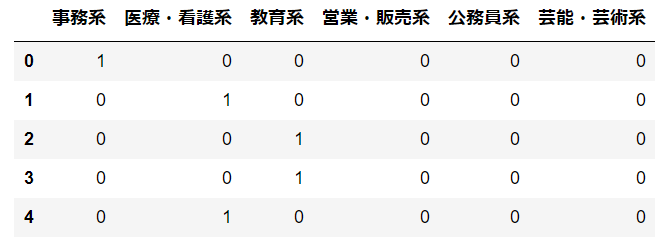
次に実際のソース例についてみていきます。
ソースコード
データの表示(ダミー変数前)
先ほどの例で示したデータがすでに入っている前提とします。
|
1 2 |
#データの表示(ダミー変数前) occupation.head() |

現時点のデータを表示しています。この段階ではまだ職業のカラムが存在します。
ダミー変数化
|
1 2 3 |
# ダミー変数化 occupation_dummy = pd.get_dummies(occupation['職業']) occupation_dummy.head() |
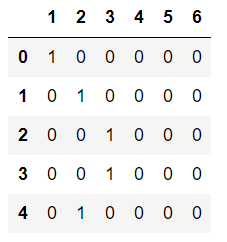
get_dummies関数を使用することによりダミー変数にすることができます。
先ほどの職業のカラムが1~6のカラムに分割されていることが分かります。
get_dummies関数の引数ですが、引数には変換したいカラムを入力してください。引数が無い場合は自動的に判断されます。その場合は数値以外のデータについてダミー変数に変換されます。
1点注意事項ですが、get_dummies関数を使用した場合元々のデータは消えてしまいます。ここでは職業のカラムが消えています。そのため後処理で職業のカラムを使用できないことに注意してください。
カラム名の付与
|
1 2 3 |
# カラム名の付与 occupation_dummy.columns = ['事務系','医療・看護系','教育系','営業・販売系','公務員系','芸能・芸術系'] occupation_dummy.head() |

新規に作成した表にはカラム名がついていないので付与しています。
多重共線性の影響をなくすために一部の列を削除
|
1 2 3 |
# 多重共線性の影響をなくすために一部の列を削除 occupation_dummy = occupation_dummy.drop(['医療・看護系','営業・販売系'],axis=1) occupation_dummy.head() |
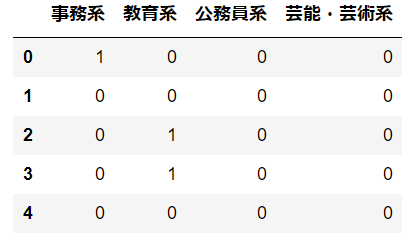
多重共線性の影響をなくすために一部の列を削除してます。
ダミー変数を行う場合の注意点(多重共線性)
ダミー変数を使用する場合1つ注意点があります。
ダミー変数同士は高度に相関する可能性があります。例えば性別のカテゴリがあり、1.男性、2.女性と定義されているとします。
その性別のカテゴリに対してダミー変数を使用した場合、新規に"男性"を示す列と"女性"を示す列が追加されます。
その場合、どちらか一方の列に1が設定されている場合、残りの列には0が設定されることになります。
このようにどちらかが決まるともう一方についても決まってしまう場合は高度に相関していることとなり、分析としてあまり良くない結果がでると言われています。
今の例では2つのカテゴリでしたが、複数のカテゴリであったも同じです。
その場合は、いくつかの列を意図的に削除することで影響を少なくすることが出来ます。
専門的には多重共線性と言われているので興味がある場合は調べてください。
ダミー変数を使用しない方がいいケース
数値に大小の連続性がある場合はダミー変数にしないようが良いと言われています。
例えば最終学歴のカテゴリがあり、1.中学、2.高校、3.専門(高専)、4.大学、5.大学院と定義されているカテゴリがあったとします。数値が大きくなれば大きくなるほど高学歴となるため、一般的には年収が高くなる傾向がありあす。その場合、最終学歴の数値の大小と年収には関連性は存在することになります。しかし、ここで最終学歴をダミー変数にした場合は独立したパラメータとなってしまうので、最終学歴と年収の関連性は薄くなってしまいます。
このように数値に大小の連続性がある場合はダミー変数にしないようが良いケースもあると言われています。