単純パーセプトロンを用いた論理演算
単純パーセプトロンを用いて論理演算を行ってみます。
単純パーセプトロンの概要については以下の記事を参照してください。
数式は以下の通りとなります。
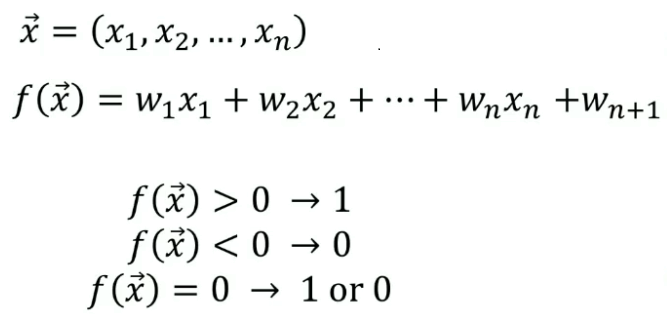
今回はコンピュータがバイアスを調整し境界線を見つけ出すまでの過程を図に示し、そのバイアス値についてどのような値になっているか確認していくことにします。
論理和(AND)
| 入力(X1) | 入力(X2) | 出力(f(x)) |
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
実行結果
境界線を特定するまでに試みた直線が緑線となり、最終的に決定した直線が黒線になります。
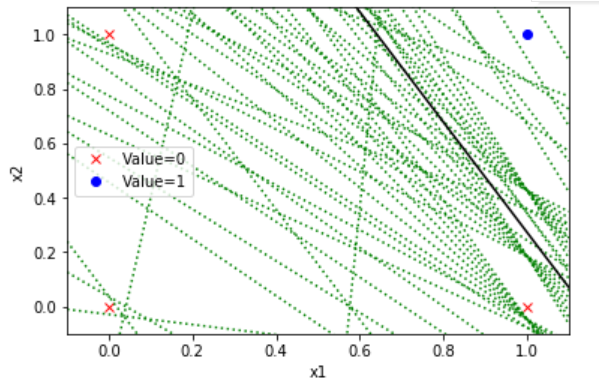
バイアス値として試みた値です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
0 : [-0.51044578 -0.20583295 0.79838035] 1 : [-0.51044578 -0.20583295 0.74838035] 2 : [-0.51044578 -0.25583295 0.69838035] 3 : [-0.56044578 -0.25583295 0.64838035] 4 : [-0.51044578 -0.20583295 0.69838035] 5 : [-0.51044578 -0.20583295 0.64838035] 6 : [-0.51044578 -0.25583295 0.59838035] 7 : [-0.56044578 -0.25583295 0.54838035] 8 : [-0.51044578 -0.20583295 0.59838035] 9 : [-0.51044578 -0.20583295 0.54838035] 10 : [-0.51044578 -0.25583295 0.49838035] 11 : [-0.46044578 -0.20583295 0.54838035] 12 : [-0.46044578 -0.20583295 0.49838035] 13 : [-0.46044578 -0.25583295 0.44838035] 14 : [-0.41044578 -0.20583295 0.49838035] 15 : [-0.41044578 -0.20583295 0.44838035] 16 : [-0.41044578 -0.25583295 0.39838035] 17 : [-0.36044578 -0.20583295 0.44838035] 18 : [-0.36044578 -0.20583295 0.39838035] 19 : [-0.36044578 -0.25583295 0.34838035] 20 : [-0.31044578 -0.20583295 0.39838035] 21 : [-0.31044578 -0.20583295 0.34838035] 22 : [-0.31044578 -0.25583295 0.29838035] 23 : [-0.26044578 -0.20583295 0.34838035] 24 : [-0.26044578 -0.20583295 0.29838035] 25 : [-0.26044578 -0.25583295 0.24838035] 26 : [-0.21044578 -0.20583295 0.29838035] 27 : [-0.21044578 -0.20583295 0.24838035] 28 : [-0.21044578 -0.25583295 0.19838035] 29 : [-0.16044578 -0.20583295 0.24838035] 30 : [-0.16044578 -0.20583295 0.19838035] 31 : [-0.21044578 -0.20583295 0.14838035] 32 : [-0.16044578 -0.15583295 0.19838035] 33 : [-0.16044578 -0.15583295 0.14838035] 34 : [-0.11044578 -0.10583295 0.19838035] 35 : [-0.11044578 -0.10583295 0.14838035] 36 : [-0.11044578 -0.15583295 0.09838035] 37 : [-0.06044578 -0.10583295 0.14838035] 38 : [-0.06044578 -0.10583295 0.09838035] 39 : [-0.11044578 -0.10583295 0.04838035] 40 : [-0.06044578 -0.05583295 0.09838035] 41 : [-0.06044578 -0.05583295 0.04838035] 42 : [-0.01044578 -0.00583295 0.09838035] 43 : [-0.01044578 -0.00583295 0.04838035] 44 : [-0.01044578 -0.05583295 -0.00161965] 45 : [ 0.03955422 -0.00583295 0.04838035] 46 : [ 0.03955422 -0.00583295 -0.00161965] 47 : [-0.01044578 -0.00583295 -0.05161965] 48 : [ 0.03955422 0.04416705 -0.00161965] 49 : [ 0.03955422 -0.00583295 -0.05161965] 50 : [ 0.08955422 0.04416705 -0.00161965] 51 : [ 0.08955422 -0.00583295 -0.05161965] 52 : [ 0.03955422 -0.00583295 -0.10161965] 53 : [ 0.08955422 0.04416705 -0.05161965] 54 : [ 0.03955422 0.04416705 -0.10161965] 55 : [ 0.08955422 0.09416705 -0.05161965] 56 : [ 0.08955422 0.04416705 -0.10161965] |
計57回で最終的な直線が決まりました。
最終的なバイアスは[ 0.08955422 0.04416705 -0.10161965]となっています。
論理積(OR)
| 入力(X1) | 入力(X2) | 出力(f(x)) |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 1 |
実行結果
境界線を特定するまでに試みた直線が緑線となり、最終的に決定した直線が黒線になります。
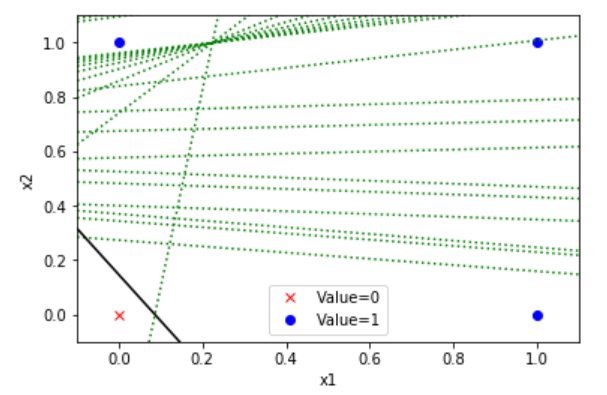
バイアス値として試みた値です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
0 : [-0.08116735 -0.70946959 0.24406528] 1 : [-0.08116735 -0.70946959 0.19406528] 2 : [-0.08116735 -0.65946959 0.24406528] 3 : [-0.03116735 -0.60946959 0.29406528] 4 : [-0.03116735 -0.60946959 0.24406528] 5 : [-0.03116735 -0.55946959 0.29406528] 6 : [ 0.01883265 -0.50946959 0.34406528] 7 : [ 0.01883265 -0.50946959 0.29406528] 8 : [ 0.01883265 -0.45946959 0.34406528] 9 : [ 0.06883265 -0.40946959 0.39406528] 10 : [ 0.06883265 -0.40946959 0.34406528] 11 : [ 0.06883265 -0.35946959 0.39406528] 12 : [ 0.06883265 -0.35946959 0.34406528] 13 : [ 0.06883265 -0.30946959 0.39406528] 14 : [ 0.06883265 -0.30946959 0.34406528] 15 : [ 0.06883265 -0.30946959 0.29406528] 16 : [ 0.06883265 -0.25946959 0.34406528] 17 : [ 0.06883265 -0.25946959 0.29406528] 18 : [ 0.06883265 -0.25946959 0.24406528] 19 : [ 0.06883265 -0.20946959 0.29406528] 20 : [ 0.06883265 -0.20946959 0.24406528] 21 : [ 0.06883265 -0.20946959 0.19406528] 22 : [ 0.06883265 -0.15946959 0.24406528] 23 : [ 0.06883265 -0.15946959 0.19406528] 24 : [ 0.06883265 -0.15946959 0.14406528] 25 : [ 0.06883265 -0.10946959 0.19406528] 26 : [ 0.06883265 -0.10946959 0.14406528] 27 : [ 0.06883265 -0.10946959 0.09406528] 28 : [ 0.06883265 -0.05946959 0.14406528] 29 : [ 0.06883265 -0.05946959 0.09406528] 30 : [ 0.06883265 -0.05946959 0.04406528] 31 : [ 0.06883265 -0.00946959 0.09406528] 32 : [ 0.06883265 -0.00946959 0.04406528] 33 : [ 0.06883265 -0.00946959 -0.00593472] 34 : [ 0.06883265 0.04053041 0.04406528] 35 : [ 0.06883265 0.04053041 -0.00593472] |
計36回で最終的な直線が決まりました。
最終的なバイアスは[ 0.06883265 0.04053041 -0.00593472]となっています。
否定論理積(NAND)
| 入力(X1) | 入力(X2) | 出力(f(x)) |
| 0 | 0 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
実行結果
境界線を特定するまでに試みた直線が緑線となり、最終的に決定した直線が黒線になります。
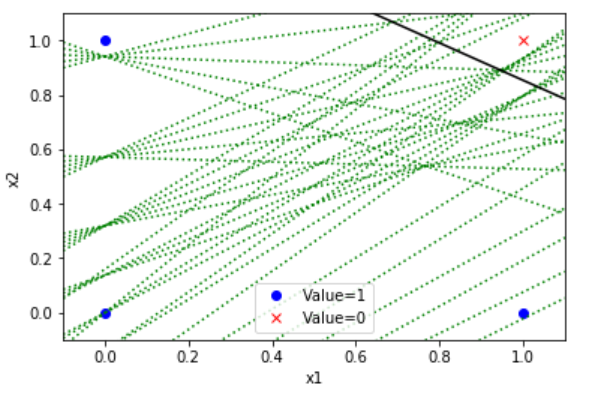
バイアス値として試みた値です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
0 : [ 0.28871669 -0.61193236 -0.70033488] 1 : [ 0.28871669 -0.61193236 -0.65033488] 2 : [ 0.28871669 -0.56193236 -0.60033488] 3 : [ 0.33871669 -0.56193236 -0.55033488] 4 : [ 0.33871669 -0.56193236 -0.50033488] 5 : [ 0.33871669 -0.51193236 -0.45033488] 6 : [ 0.38871669 -0.51193236 -0.40033488] 7 : [ 0.38871669 -0.51193236 -0.35033488] 8 : [ 0.38871669 -0.46193236 -0.30033488] 9 : [ 0.38871669 -0.46193236 -0.25033488] 10 : [ 0.38871669 -0.41193236 -0.20033488] 11 : [ 0.38871669 -0.41193236 -0.15033488] 12 : [ 0.38871669 -0.36193236 -0.10033488] 13 : [ 0.38871669 -0.36193236 -0.05033488] 14 : [ 3.88716692e-01 -3.11932362e-01 -3.34884471e-04] 15 : [ 0.33871669 -0.36193236 -0.05033488] 16 : [ 3.38716692e-01 -3.61932362e-01 -3.34884471e-04] 17 : [ 0.33871669 -0.31193236 0.04966512] 18 : [ 2.88716692e-01 -3.61932362e-01 -3.34884471e-04] 19 : [ 0.28871669 -0.36193236 0.04966512] 20 : [ 0.28871669 -0.31193236 0.09966512] 21 : [ 0.23871669 -0.36193236 0.04966512] 22 : [ 0.23871669 -0.31193236 0.09966512] 23 : [ 0.18871669 -0.36193236 0.04966512] 24 : [ 0.18871669 -0.31193236 0.09966512] 25 : [ 0.18871669 -0.26193236 0.14966512] 26 : [ 0.13871669 -0.31193236 0.09966512] 27 : [ 0.13871669 -0.26193236 0.14966512] 28 : [ 0.08871669 -0.31193236 0.09966512] 29 : [ 0.08871669 -0.26193236 0.14966512] 30 : [ 0.08871669 -0.21193236 0.19966512] 31 : [ 0.03871669 -0.26193236 0.14966512] 32 : [ 0.03871669 -0.21193236 0.19966512] 33 : [-0.01128331 -0.26193236 0.14966512] 34 : [-0.01128331 -0.21193236 0.19966512] 35 : [-0.01128331 -0.16193236 0.24966512] 36 : [-0.06128331 -0.21193236 0.19966512] 37 : [-0.06128331 -0.16193236 0.24966512] 38 : [-0.11128331 -0.21193236 0.19966512] 39 : [-0.11128331 -0.16193236 0.24966512] |
計40回で最終的な直線が決まりました。
最終的なバイアスは[-0.11128331 -0.16193236 0.24966512]となっています。
排他的論理和(XOR)
| 入力(X1) | 入力(X2) | 出力(f(x)) |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 1 | 0 |
実行結果
この排他的論理和(XOR)については単純パーセプトロンではできません。
境界線を分ける直線をひくことが出来ないためです。
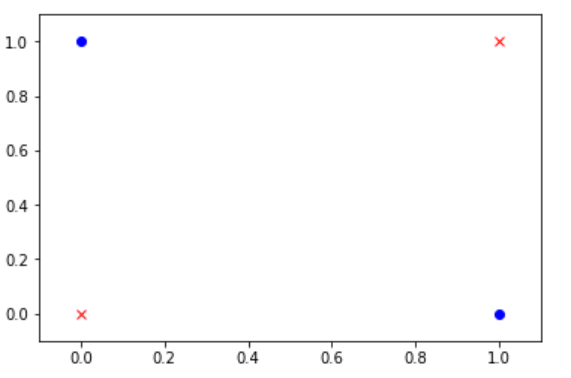
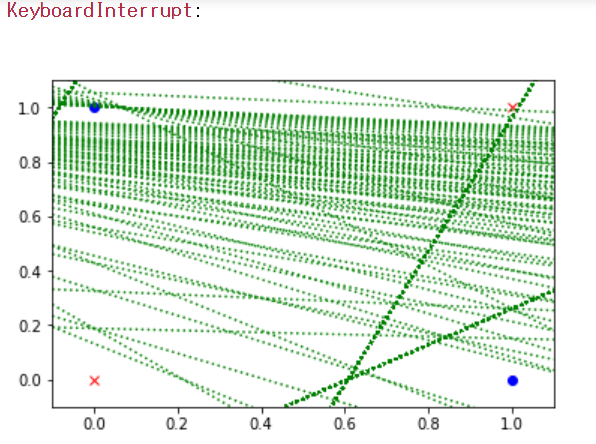
これが単純パーセプトロンの限界になります。
